前言

昨天我們實作策略迭代 (Policy Iteration)，在實作中，我們重複進行「策略評估」與「策略增進」這兩個步驟。那麼，我們有沒有辦法把這兩個步驟合併嗎？

價值迭代 (Value Iteration)

這個方法希望將「策略評估」與「策略增進」這兩個步驟合併。價值評估函數的形式，我們在 Day 9 說明貪婪法時，已經呈現過。

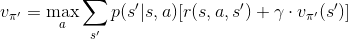
只是在策略迭代的方法中，我們使用「策略增進」來決定最佳的動作，並送到「策略評估」中。然而在價值迭代的方法中，我們在評估狀態價值時，不再像「策略評估」只執行最好的動作，而是計算所有動作，並選擇價值最高者，做為新的狀態價值。演算法如下所示：

(取自 Sutton 書籍)

不好意思，今天才注意到 Sutton 網路版與 pdf 版的符號表示不同，找個時間會回去更新。

以下分成三個部分，來說明我們實作使用價值迭代於 GridWorld 的過程，完整程式請見 GitHub。

• 價值迭代
  Value Iteration 實作的方法也很簡單，就只是將兩者(「策略評估」與「策略增進」)合併起來。

def ValueIteration(func_value, func_reward, trans_mat, gamma):
    best_action = np.zeros(16)
    func_value_now = func_value.copy()
    for state in range(1,15):
        next_state = trans_mat[:,state,:]
        future_reward = func_reward + func_value*gamma
        func_value[state] = np.max(np.matmul(np.transpose(next_state), future_reward))
        best_action[state] = np.argmax(np.matmul(np.transpose(next_state), future_reward))
    delta = np.max(np.abs(func_value - func_value_now))
    return func_value, delta, best_action

值得注意的是，我們 不需要 考慮各狀態下各動作出現的機率，因為我們只選擇最好的動作。

• 主程式
  主程式的部分，一樣先設定強化學習中所需要的參數、終止條件，剩下的就是在迴圈中更新狀態價值與動作策略。

def main():
    ## environment setting
    # action
    ProbAction = np.zeros([16,4])
    ProbAction[1:15,:] = 0.25
    # value function
    FuncValue = np.zeros(16)
    # reward function
    FuncReward = np.full(16,-1)
    FuncReward[0] = 0
    FuncReward[15] = 0
    # transition matrix
    T = np.load('./gridworld/T.npy')

    # parameters
    gamma = 0.99
    theta = 0.05
    delta = delta = theta + 0.001
    counter_total = 0

    # iteration
    while delta > theta:
        counter_total += 1
        os.system('cls' if os.name == 'nt' else 'clear')
        ValueFunc, delta, BestAction = ValueIteration(FuncValue, FuncReward, T, gamma)
        ShowValue(delta, theta, gamma, counter_total, FuncValue)
        PolicyString = ShowPolicy(counter_total, BestAction)
        time.sleep(2)

    os.system('cls' if os.name == 'nt' else 'clear')
    print('='*60)
    print('Final Result')
    print('='*60)
    print('[State-value]')
    print(FuncValue.reshape(4,4))
    print('='*60)
    print('[Policy]')
    print(PolicyString.reshape(4,4))
    print('='*60)

• 實驗結果
  經過計算後，我們可以獲得和昨天一樣的結果。

============================================================
Final Result
============================================================
[State-value]
[[ 0.    0.   -1.   -1.99]
 [ 0.   -1.   -1.99 -1.  ]
 [-1.   -1.99 -1.    0.  ]
 [-1.99 -1.    0.    0.  ]]
============================================================
[Policy]
[['*' '<' '<' '<']
 ['^' '^' '^' 'v']
 ['^' '^' 'v' 'v']
 ['^' '>' '>' '*']]
============================================================

至此，我們將動態規劃方法中的「策略迭代」與「價值迭代」方法介紹完了。明天，我們來討論動態規劃方法的一些優缺點。